サスペンションと車体にかかる力
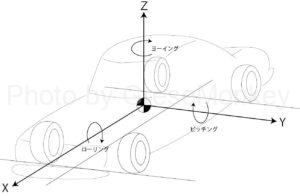
サスペンションが制御するクルマの挙動は、上図に示すX軸、Y軸、Z軸上で、それぞれローリング、ピッチング、ヨーイングの3つの動きに分けられる。この動きのうち、クルマを側面からみたときの動き、すなわちY軸を中心とした前後の動きであるピッチングについて考えてみる。
目次
サスペンションアームが引き起こす力
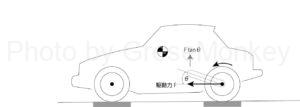
FR方式のクルマで、Dレンジに入れたり、アクセルを踏み込んで加速をしたりした場合に、車体の後部がググッと尻下がりになった経験があると思うが、これには2つの力が作用している。
1つは加速を妨げようとする慣性力である。クルマは加速させようとすると、その加速させる直前の走行状態(低速であったり減速であったり。)をそのまま保とうとする力が働く、この加速直前の状態をそのまま保とうとして車体に働く力を慣性力という。
この力はクルマが加速することで、車体に作用する力が変化しようとすると、それを元の状態に戻そうとする方向に作用する。つまり、加速させようとすると、その逆に加速させまいとして作用する。
2つめは、車輪にかかる駆動力である。これはその名の通りクルマの加速に比例して増大する。
この2つの力が、加速時の車体に尻下がりの力を発生させる。そして、この尻下がりの動きを押さえようとするのが、アンチスクワットである。
アンチスクワット力
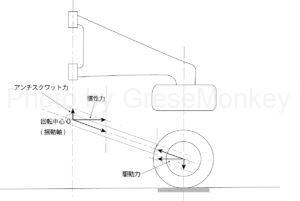
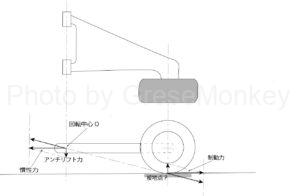
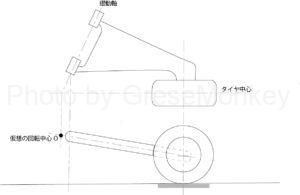
フルトレーリングアーム式サスペンションの場合、加速時ではタイヤはサスペンションアームに対して自由に回転できる状態なので、駆動力は車輪の中心に作用することになる。(図1参照)
このとき、サスペンションアームの揺動軸(回転軸)は、タイヤ(中心)が回転運動するときの回転中心になる。そして駆動力は、サスペンションアームの揺動軸(回転中心O)を押し上げようとする力を発生させる。
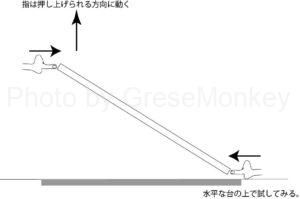
例えば図2のように、台の上で縦方向の動きを固定した状態で、棒の片側を押すと、反対側は持ち上げられるように力が働くのと同じ原理になる。
この車体を押し上げようとする力が、加速時の車体後部を押し下げようとする力に対して反対方向に作用する。つまり、尻下がりの動きを押さえようとするアンチスクワット力として働く。
このアンチスクワット力は、本来ならば回転中心O(揺動軸:車体の取り付け点)に働くはずであるが、車体全体に比べるとサスペンションアームの長さは短いので、タイヤ中心上に作用すると見なしても大きな差異はない。
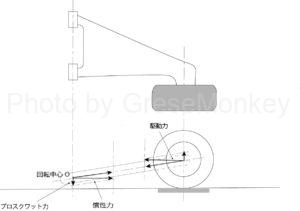
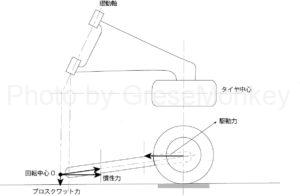
図3のように、回転中心Oが車輪の中心より低い場合には、駆動力は車体を押し下げようとする力を発生させる。この場合にはスクワット(尻下がりの力)を促すように働くので、プログレス・スクワットとか、プロスクワットなどと呼ぶことがある。
図4のように、ブレーキを掛けたときの場合を考えてみる。ブレーキを掛けたときはサスペンションアームに固定されたキャリパーがタイヤの回転を止めようとして、タイヤが自由に回転できない状態になるので、制動力はタイヤの接地点に作用することになる。このとき、制動力は回転中心O(揺動軸)を押し下げるように作用する。つまり、この力がアンチリフト力として働くことになる。
加速時に車体に働く力
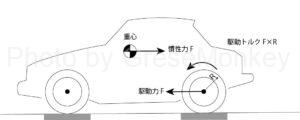
加速時の尻下がり現象で、車体のお尻を下げようとする力は次のように考えていく。(図5参照)
駆動力Fはタイヤの接地点に作用するが、この力はタイヤ中心に働く前向きの力Fと、駆動トルクF×Rに分けて考える事ができる。ここで、Rはタイヤの半径を指す。
先にのべたように、フルトレーディングアーム式サスペンションの場合では、タイヤはサスペンションアームに対して自由に回転できる状態なので、この駆動トルクF×Rはサスペンションには伝わらすに、タイヤの回転軸上のデファレンシャルギヤを介して車体に伝わることになる。
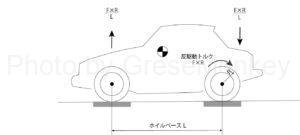
このとき、この駆動トルクをホイールベースLで除した(F×R)/Lの力で前輪側を持ち上げ、後輪側を押し下げようとする。(図6参照)
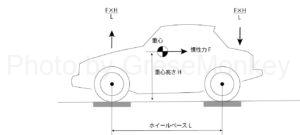
加速により発生する慣性力は駆動力に等しいが、車両の重心に作用することになるので、重心の高さをHとすると、(F×H)/Lの力で前輪側を持ち上げて、後輪側を押し下げようとする。(図7参照)
また一方で、車輪の中心に働く前向きの力(駆動力)は、サスペンションアームの傾きによっては逆に押し下げようとするが、基本的には車体後部を押し下げようとする。そのときの力はF×tanθとなり、これがアンチスクワット力となる。(図8参照)
そこで、前輪側を押し上げ、後輪側を押し下げようとするスクワット力は、2つの力の和で表すことができ、
$$\frac{F×R}{L}+\frac{F×H}{L} $$
となる。したがって加速時のスクワットをゼロにするためには、スクワット力とアンチスクワット力を等しくすれば良いので、
$$ \frac{F×R}{L}+\frac{F×H}{L}=F×\tan\theta $$
$$ ∴ \frac{R+H}{L}=F×\tan\theta $$
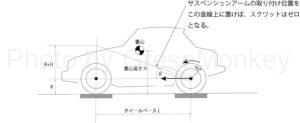
となるようにサスペンションアームの取り付け位置を決定すれば良いということになる(図9参照)
すなわち、図9のように、前輪中心にタイヤ半径と重心高さを加えた点と、後輪中心を結んだ直線上にあれば良いということになる。
セミトレーリングアーム式の場合
セミトレーリングアーム式の場合の回転中心Oを求めるには、最初に、セミトレーリングアームを上から見た図(平面図)でサスペンションアームの車体側の取り付け点(揺動軸)を直線で結んで延長し、タイヤ中心線の延長戦と交差した点が平面図上での回転中心Oとなる。(図10参照)
この平面図上での回転中心Oから垂線を下ろし、タイヤを横から見た図(側面図)のサスペンションアームを延長した直線と交差した点。これがセミトレーリングアーム式の場合の回転中心Oとなる。
つまり、セミトレーリングアーム式の場合の回転中心は、実際には揺動軸が存在しない仮想の回転中心となる。(実体の中心が車体に存在しない)これはロールセンターを求めた時の瞬間中心と同じような考え方である。
回転中心Oを求めた後はトレーリングアーム式の場合と全く同じで、回転中心Oとタイヤに作用する力との位置関係によってアンチスクワットやアンチリフトが決定する。
セミトレーリングアーム式のキャンバー変化は、タイヤが揺動軸と同じ高さの位置(水平状態)から上にバウンド(バンプ)ストロークするとネガティブキャンバーとなり、下にリバウンドするとポジティブキャンバーとなる。
また、トー変化は、バウンドストロークでもリバウンドストロークでもトーイン傾向となる。そのため、揺動軸を車軸中心より下に設定して、ネガティブキャンバーとなる領域を多く使えるようにするケースが多く見られる。
こうすると、加速時のスクワット状態を促進することになってしまうのだが、セミトレーリングアーム式でアンチスクワット特性を与えることは難しい。たとえば、FR方式のクルマで、揺動軸の位置を高く設定しようとすると、リヤシートやフロアに邪魔されて、設定の自由度が難しくなる。セミトレーリングアーム式を用いたFR方式のクルマにおいて、加速時に尻下がり現象が起こるのは、アンチスクワット特性を与えにくい構造であるからである。サスペンション方式の変更や改良、設計の自由度などを見直していくことで、今後の改善が期待される。
引用元・参考文献・Webサイト
このサイトのテキストは一部以下の著作・出版物・Webサイトより引用させて頂きました。
・「車両運動性能とシャシーメカニズム」宇野高明著 グランプリ出版
・「サスペンションの仕組みと走行性能」熊野学著 グランプリ出版


“サスペンションと車体にかかる力” への1件のフィードバック