自動車の走行性能
目次
自動車の走行性能
自動車が走行する際には、複数の抵抗が発生する。その中でも主要なものは、転がり抵抗、空気抵抗、勾配抵抗、および加速抵抗である。
転がり抵抗はタイヤと路面の間の摩擦によるもので、空気抵抗は車両が進行する際に空気との摩擦で生じる。
勾配抵抗は坂道を登る際に重力が引き起こす抵抗で、加速抵抗は速度を上げる際に必要な力である。
これらの抵抗力はすべて走行を妨げる方向に作用し、これらを総称して走行抵抗と呼ぶ。
走行抵抗とは対照的に、自動車が前進するための力が駆動力である。この力はエンジンから発生するトルクによって生み出され、自動車が進行するためにはこの駆動力が走行抵抗を上回る必要がある。
具体的には、エンジンが生成する動力がギアボックスを介して車輪に伝達され、車両を動かす。この駆動力の大きさと効率は、車両の加速性能や坂道での性能に直接影響を与える。

図1:走行性能曲線図
図1の「走行性能曲線図」は、自動車の走行性能を視覚的に表現したものである。
この図は、車速と駆動力、エンジンの回転速度との関係を線図で示している。この図からは、車両の加速能力や登坂能力、最高速度などの性能を詳しく理解することができる。
たとえば、エンジンの回転速度が一定のときにどの程度の駆動力が発生するか、あるいは特定の速度でのエンジンの効率などが読み取れる。これにより、自動車の性能を最適化するための重要な情報が得られる。
走行抵抗と駆動力
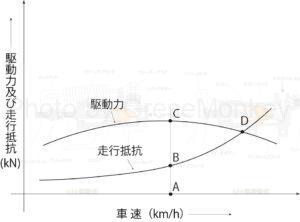
図2:走行抵抗と駆動力
図2は、トップギヤで平坦な路面を走行する自動車の車速とそれに対応する走行抵抗及び駆動力の関係を示している。図内の車速が点Aのとき、駆動力は点Cに位置し、走行抵抗は点Bに位置する。このとき、駆動力Cは走行抵抗Bを上回っており、その差分が余裕駆動力となる。この余裕駆動力は、車が平坦な路面を走行する際に加速力として作用する。
車が登り坂を走行する際には、この余裕駆動力が登坂力として作用する。しかし、坂の勾配が大きくなるにつれて、勾配抵抗が増大し、結果として余裕駆動力は減少する。車速が上昇し続けると、図の点Dにおいて駆動力と走行抵抗が等しくなり、これ以上の速度増加は起こらず、速度は一定となる。このときの速度を最高速度という。
以上から、駆動力、走行抵抗、および余裕駆動力の関係は次の式で表される。
この式は、車両の性能を数値的に理解するための基本となり、車両の加速性能や最高速度などを評価する際に重要な指標となる。
走行抵抗
走行抵抗とは、自動車が移動する際に克服しなければならない複数の抵抗の総称である。具体的には以下の4つの要素から成り立っている。
自動車が走行する際にタイヤが路面から受ける抵抗
自動車が走行する際に起こる空気の流れなどから受ける抵抗
坂路を上るまたは下るときなどに自動車が受ける抵抗
アクセルを踏み込んで自動車が加速した際に受ける様々な抵抗
これらの抵抗は、自動車が効率よく走行するために必要となってくる抵抗で、エネルギー効率、燃費、加速性能、最高速度などの車両性能に直接影響を与える。車両の設計時には、これらの走行抵抗を最小化することで、性能を最大化し、燃料消費を抑えることが求められる。
転がり抵抗
転がり抵抗はタイヤが路面を転がる際に生じる抵抗力で、タイヤと路面の接触によるエネルギーの損失が主な原因である。タイヤの材質、空気圧、路面の質、タイヤの温度などの条件によって影響を受ける。転がり抵抗は走行速度が増加するにつれて増大するが、その増加率は比較的小さくなる。
この抵抗力は、主に以下の要因によって発生する。
自動車が静止しているときのタイヤの接地面はタイヤ接地部と呼ばれる。この部分はタイヤの形状や空気圧によって変化し、また路面の質や形状に応じて接地する面積や形状が変わる。タイヤが回転すると、接地部が連続して変形し、この変形によって抵抗が生じる。
自動車が走行する際には、タイヤのトレッド部分が路面に接触し、この接触部分に摩擦力が発生する。タイヤの材質やトレッドのパターン、路面の状態などによって摩擦の大きさが変わり、この摩擦力が転がり抵抗を生じさせる。
タイヤの回転軸である軸受部にも摩擦が生じる。これはホイールと車体を繋ぐベアリングによるもので、ベアリング自体の構造や潤滑状態によって抵抗の大きさが変わる。この部分の摩擦も転がり抵抗の一部となる。
路面が完全な平面ではないため、段差やカーブなどの不規則な形状を走行する際には、通常の直進状態とは異なる抵抗が生じる。これはタイヤが路面の変形に対応するために追加のエネルギーを必要とするためである。
これらの要因は、タイヤの走行抵抗として総合的に働き、自動車の燃費や動力性能に影響を与える。したがって、車両の設計やメンテナンスにおいて、これらの抵抗を最小限に抑えることが重要である。
転がり抵抗は、自動車の重量や路面の状況によって左右され、様々な要素があるのだが、一般的に平坦な路面での転がり抵抗の計算は、次の式で表される。
$$ R1 = \mu Mg $$
ただし、
\( R1 \):転がり抵抗\(N\) = \(kg\)・\(m/s\)\(^2\) = \(kg\)・\(m\)・\(s\)\(^{-2}\)
\( \mu \):転がり抵抗係数
\( M \):自動車総質量(\(kg\))
\( g \):重力加速度 = 9.8 \(m/s\)\(^2\) = 9.8\( m\)・\(s\)\(^{-2}\)
路面の状況による影響
転がり抵抗係数は、次の表1に示す。
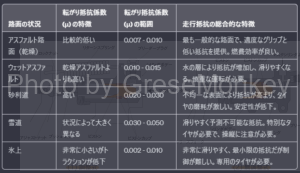
表1:路面の状況と転がり抵抗係数
– 転がり抵抗係数の「係数」とは
係数とはある現象の法則性を説明するときに、一個以上の変数の式を用いる場合、その変数を用いた式にかかっている定数のことで、その定数は場合によって変化する。
例えば、上記の転がり抵抗の計算式(\(R1 = \mu Mg\))での変数は求める転がり抵抗\(R1\)と自動車総質量\(M\)の2つだけである。
この変数のうち転がり抵抗R1は、表1の路面の状況によって変化する係数(定数)\(\mu\)と不変の定数である重力加速度\(g\)(=9.8\(m/s^2\))に変数である自動車総重量\(M\)の3つを掛け合わせることで求めることができる。
ここで、同じ車で様々な路面状況での転がり抵抗を求めることを考えると、自動車総重量\(M\)は一定の値とする必要があるので、変数から定数として扱うことが出来る。
路面の状況を選択してその転がり抵抗係数である\(\mu\)の値を決めてしまうことができれば、あとは\(R1 = \mu Mg\)の式にそれぞれの値を代入すれば、転がり抵抗は必然的に決定される。
車速による影響
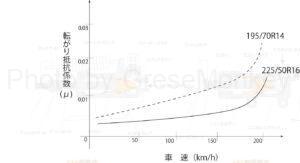
図3:車速と転がり抵抗係数の関係
転がり抵抗係数は、図3より、ある車速以上になると急激に上昇する傾向がある。
この原因はタイヤのスタンディングウェーブの発生によるものである。
スタンディングウェーブとは、タイヤが持続的に荷重を受けることで生じる現象である。自動車のタイヤは、常に車両の荷重によってたわんだ状態を保っている。
タイヤの空気圧が適正でない場合や車両が過積載により重たくなった場合、タイヤのたわみはより大きくなる。この状態で高速走行を続けると、タイヤ内部でたわみが多重に重なり合い、波打つような状態、すなわちスタンディングウェーブが生じる。この状態が続くと、タイヤのバーストなどの重大なトラブルの原因となる可能性がある。
しかし、タイヤの空気圧が適正であっても、高速走行ではスタンディングウェーブは発生しうる。
タイヤは完全な真円ではなく、適切な状態であってもわずかにたわんでいるためである。運転者が意識していなくても、このたわみがスタンディングウェーブの原因となり得る。
ただし、タイヤは適切な空気圧や取付状態を前提として、一定の高速走行においてもトラブルが起こらないように設計開発されている。したがって、タイヤの適切なメンテナンスと定期的なチェックが重要であり、これによりスタンディングウェーブによるトラブルを防ぐことができる。
タイヤの変形量による影響
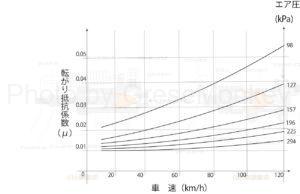
図4:タイヤのエア圧及び車速と転がり抵抗係数の関係
タイヤの空気圧が高いほどタイヤの変形が小さくなるので、転がり抵抗係数は小さくなる。
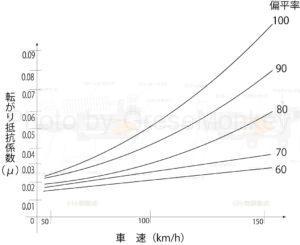
図5:偏平率と転がり抵抗係数の関係
タイヤの偏平率が小さいほどタイヤの変形が小さくなるので、転がり抵抗係数は小さくなる。
タイヤの扁平率
タイヤの扁平率(%) = (タイヤの断面高さ ÷ 断面幅) ✕ 100
タイヤの偏平率は、簡単に言えばタイヤの偏平度。つまり、タイヤを真横から見たときにホイール端面とタイヤの端面までの高さが低ければ低いほど偏平率が低いタイヤとなるのだが、こういったタイヤは、路面とタイヤの接地部分の面積(トレッド)が広く、ノーマルなタイヤよりも硬めに作られていることがほとんどなので、高速走行でもタイヤの変形が少なく、なおかつ走行安定性も良い。
一方で、偏平率の高いタイヤはホイール端面からタイヤ端面までの距離が高く、衝撃を吸収するように柔らかめに作られている。そのため、高速走行時では変形しやすく、転がり抵抗も増大しやすいのだが、偏平率が低いタイヤよりも乗り心地が良い。
坂路による影響
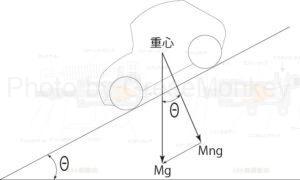
図6:坂路における垂直荷重
図6のような坂路においては、自動車総質量 ✕ 重力加速度(\(Mg\))の分力である坂路の路面に垂直な荷重(\(Mng\))は、勾配角度Θが大きくなるにつれて減少する。
この関係は次式で表される。
$$Mng = Mg\cos\theta$$
$$R1 = \mu Mg \cos\theta$$
ただし
\(R1\):坂路の転がり抵抗 \(N\)=\(kg\)\(m/s\)\(^2\)
\(\mu\):転がり抵抗係数
\(M\):自動車総質量
\(g\):重力加速度 \(9.8m/s\)\(^2\)
\(\theta\):勾配角度
空気抵抗
空気抵抗は自動車が空気を押しのけて進む際に生じる抵抗で、自動車の形状、表面の滑らかさ、車速などによって変化する。速度の増加に伴い、空気抵抗の力は速度の2乗に比例して増加するため、高速で走行するほどその影響は大きくなる。
直進時で自然風がないとき、車体には抗力(進行方向と反対の力)、揚力(上昇しようとする力)、横力(進行方向に対して垂直方向の力)が作用している。
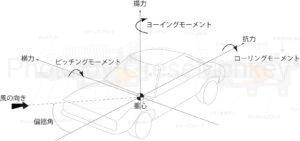
図7:車体に作用する力
図7のように、自然風が吹いてきたり、自動車が旋回した場合などには、この図の3方向の力(抗力・揚力・横力)に加えて、ヨーイングモーメント、ローリングモーメント及びピッチングモーメントが作用してくるため、自動車の操縦性、安定性に大きな影響が及んでくることになる。
抗力、揚力、横力は、自動車の運動に影響を及ぼす三つの主要な空気力である。
抗力は、車体に対して後方へ作用する力である。車が進行すると、車体前部で受けた空気が正圧を生じ、一方で後部で空気が剥離することにより負圧が生じる。これら正圧と負圧の組み合わせが、車体を後方へ引く力、すなわち抗力として働く。この抗力は車両の速度に比例して増加し、燃費や最高速度に直接的な影響を与える。
揚力は、車体に垂直に上向きに作用する力である。車体の上面と下面を流れる空気の速度差により生じる圧力差が原因で、車体が持ち上げられる方向に力が働く。揚力が大きくなると、タイヤの路面への接地力が減少し、それにより操縦安定性が低下する。特に高速走行時に揚力が問題となることが多く、レーシングカーや高性能車では、この揚力を抑制するために空力デザインが重視される。
横力は、車体の横方向に作用する力である。この力は主に横風によって生じ、風向きの変化(偏揺角)に比例して大きくなる。横力は車両の横滑りや進行方向の変化を引き起こし、ドライバーにとっては予期せぬ挙動を招く可能性がある。特に高速道路などでの横風の影響は大きく、横力による操縦の乱れは運転の安全性に直結する。
空気抵抗は、自動車の前面投影面積及び対気速度の2乗に比例し、次式で表される。
$$R2 = \frac{1}{2} Cd Av^2\rho$$
ただし
\(R2\):空気抵抗 \(N\) = \(kg\)・\(m/s\)\(^2\)
\(Cd\):空気抵抗係数
\(A\):全面投影面積 \(m\)\(^2\)
\(v\):対気速度 \(m/s\)
\(\rho\):空気密度 \(kg/m\)\(^3\)
なお、空気抵抗係数は、車体の形状によって異なる(表2)
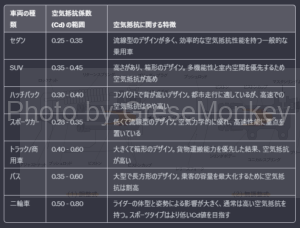
表2:自動車の空気抵抗係数
注1)対気速度:自動車の速度と風速との合成速度のこと
注2)空気密度は標準待機状態(1気圧・15℃)で、1.225kg/m\(^2\)である
勾配抵抗
勾配抵抗は坂道を登る際に生じる抵抗で、坂の勾配の大きさと重力が関係している。この抵抗は坂道の角度に直接比例し、車速とは独立している。坂道が急であるほど、勾配抵抗は大きくなる。
自動車が坂路を上る場合には、自動車の重量の分力が駆動力に対して反対の向きに作用する。
これを勾配抵抗という。図8のように、重量(\(Mg\))の自動車が勾配角度Θの坂路を上る場合、重力の分力(\(R3\))が勾配抵抗で、次の式で表される。
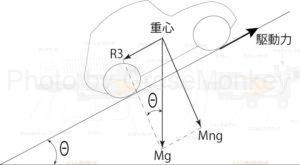
図8:勾配と勾配抵抗
$$R3 = Mg・sin\theta$$
ただし
\(R3\):勾配抵抗 \(N\) = \(kg\)・\(m/s\)\(^2\)
\(M\):自動車総質量 \(kg\)
\(g\):重力加速度 = 9.8\(m/s\)\(^2\)
\(\theta\):勾配角度
道路の勾配は、一般に\(\tan\theta\)で表すため、勾配抵抗を計算するには、\(tan\theta\)から\(sin\theta\)を求める必要がある。
ただし、\(\theta\)が小さい時は近似的に\(sin\theta ≒ tan\theta\)とみなしても実用上差支えない。
例えば、自動車総質量1225kgの自動車が10%の勾配を上がるときの勾配抵抗を計算する場合
\(\tan\theta ≒ \sin\theta\) とみなすと
\(\tan\theta = 0.1\) であることから \(\sin\theta = 0.1\)
勾配抵抗 \(R3 = Mg \cdot \sin\theta\) より
\(R3 = 1225 \, \text{kg} \times 9.8 \, \text{m/s}^2 \times 0.1 = 1200.5 \, \text{N}\)
よって \(R_3 = 1200.5 \, \text{N}\)
以上のことから、自動車には約1200Nの力で後方に惹かれているのと同じ勾配抵抗がかかっていることになる。
これは、走行に伴い、自動車の質量を高い位置に持ち上げる仕事が加わるためである。
勾配抵抗は、車速に関係なく一定値であるが、勾配が変化することにより抵抗も変化するため、図9のような特性を示すようになる。
なお、下り勾配の場合では、勾配抵抗が負となり走行抵抗を減らすので、駆動力を助ける力として働く。

図9:登り勾配の勾配抵抗
加速抵抗
自動車が加速するときに発生する抵抗を加速抵抗といい、慣性の法則によって加速しようとする力に対して発生する抵抗のことである。
加速抵抗は自動車が加速する際に必要な追加の力で、自動車が速度を変えるためには、慣性を克服するための力が必要となる。この抵抗の大きさはアクセルの踏み込み具合や車両の加速度によって決まり、運転者の運転技術によっても影響を受ける。急激な加速を行うほど、加速抵抗は大きくなる。
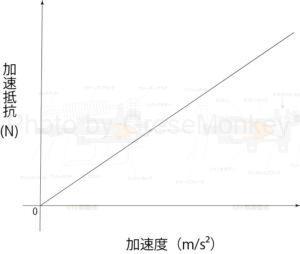
図10:加速抵抗と加速度の関係
したがって、この加速抵抗は、加速した自動車を減速する方向に作用する。
加速抵抗は次の式で表される。
$$R4 = M\alpha + M’\alpha = (M + M’)\alpha$$
ただし
\(R4\):加速抵抗 \(\text{N} = \text{kg} \cdot \text{m/s}^2 = \text{kg} \cdot \text{m} \cdot \text{s}^{-2}\)
\(\alpha\):加速度 \(\text{m/s}^2\)
\(M\):自動車総質量 \(\text{kg}\)
\(M’\):回転部分相当慣性質量 \(\text{kg}\)
駆動力と走行性能
駆動力を大きくすることが出来れば、登坂や加速の能力が増大し、最高速度も高くなる。
駆動力は、エンジンのトルクまたは動力伝達装置の減速比を大きくするか、駆動輪の直径を小さくすることにより増大させることが出来る。
しかし、駆動力は路面とタイヤの摩擦力が超えると空転してしまい、動力を有効に伝えることが出来ない。
したがって、駆動力の最大限度は次の式で表すことが出来る。
$$F0 = \mu Mg$$
ただし
\(F0\):駆動力の最大限度 \(\text{N} = \text{kg} \cdot \text{m/s}^2 = \text{kg} \cdot \text{m} \cdot \text{s}^{-2}\)
\(\mu\):路面とタイヤとの間の摩擦係数
\(M\):駆動輪にかかる質量の総和 \(\text{kg}\)
\(g\):重力加速度 \(9.8 \, \text{m/s}^2 = 9.8 \, \text{m} \cdot \text{s}^{-2}\)
摩擦係数(\(\mu\))については、路面とタイヤの状態によって変化する。(表3)

表3:摩擦係数
駆動力には各駆動輪ごとに限界がある。
登坂能力、加速能力や最高速度などといった走行性能を最大限に発揮するには、四輪駆動式(4WD)方式が有利であるが、そのほかにも自動車の形状、材質などの改良により走行抵抗を最小限に抑えることが有効になってくる。
走行性能
走行性能曲線図
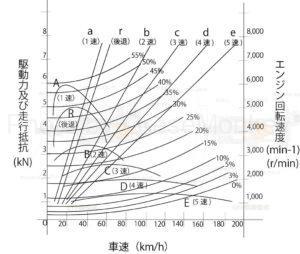
図11:走行性能曲線図
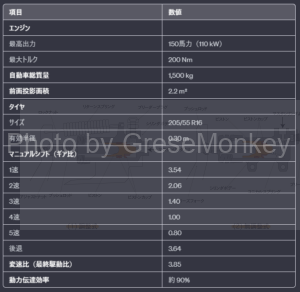
表4:一般的な自動車の諸元表
図11は、表4の諸元表に示す性能を持ち合わせた自動車の走行性能曲線図を示したものである。
横軸を車速(\(km/h\))、縦軸に駆動力及び走行抵抗(\(kN\))及びエンジン回転速度(\(\text{min}^{-1}\))を示している。
図11において示している要素は次のとおりである。
- A~E及びRは、それぞれシフトの1速から5速及び後退の車速における駆動力
- 0~55%は上り坂での車速における走行抵抗
- a~e及びrは車速におけるエンジン回転速度
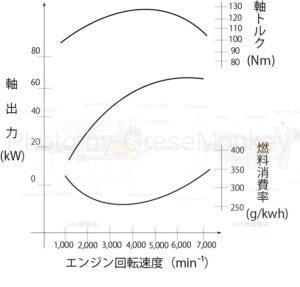
図12:エンジン性能曲線図
図12は、図11の走行性能曲線図で示した自動車のエンジン性能曲線図である。
図12から、このエンジンが回転速度1000~6500\(\text{min}^{-1}
\)の範囲で約90~120\(N・m\)の軸トルクを出力することがわかる。
一般的に、エンジンのトルクと自動車の駆動力との間には、次のような関係がある。
$$F = \frac{Te \cdot i \cdot \eta}{r}$$
ただし
\(F\):駆動力 \(\text{N}\)
\(Te\):エンジンのトルク \(\text{N} \cdot \text{m}\)
\(i\):総減速比
\(\eta\)(イータ):動力伝達効率
\(r\):駆動輪タイヤの動荷重半径 \(\text{m}\)
この式から、自動車の駆動力はエンジンのトルク、総減速比及び動力伝達効率に比例し、駆動輪タイヤの動荷重半径に反比例することがわかる。
また、エンジンの回転速度と車速との間には次のような関係がある。
駆動輪が1回転する間に自動車が進む距離は、タイヤの動荷重半径を\(r\) [\(m\)]とすると、\(2\pi r\) [\(m\)]になる。
つまり、駆動輪が\(Nr\) [\(\text{min}^{-1}\)]回転すると、1時間に進む距離は、\(Nr \cdot 60\) [\(\text{h}^{-1}\)] \(\cdot 2\pi r\) [\(m\)]となる。
したがって、車速(\(v\))を\(km/h\)で求めるために(換算)\(10^3\) [\(m\)] \(\cdot\) [\(\text{km}^{-1}\)]で割ると
\(v = \frac{Nr \cdot 60 \cdot 2\pi r}{10^3}\) [\(km/h\)]
よって \(v = \frac{Nr \cdot 60 \cdot 2\pi r}{10^3}\) [\(km/h\)] —➀
また、\(Nr = \frac{Ne}{i}\) (エンジン回転速度) であるので、エンジン回転速度と車速との関係は
\(v = \frac{Nr \cdot 60 \cdot 2\pi r}{10^3}\) [\(km/h\)]に \(Nr = \frac{Ne}{i}\) を代入すると
\(v = \frac{Ne \cdot 60 \cdot 2\pi r}{10^3 \cdot i}\) [\(km/h\)]となる。
よって \(v = \frac{Ne \cdot 60 \cdot 2\pi r}{10^3 \cdot i}\) [\(km/h\)] —➁
この2つの式➀、➁に表4の諸元表と図12のエンジン回転速度とトルクの数値を当てはめることで、車速と駆動力及びエンジン回転速度の関係を算出することができる。
また、駆動力と車速及び出力の関係を見ると、次の式が成立する。
$$P = Fv$$
ただし
\(P\):出力 \(\text{W} = \text{kg} \cdot \text{m}^2/\text{s}^3 = \text{kg} \cdot \text{m}^{-2} \cdot \text{s}^{-3}\)
\(F\):駆動力 \(\text{N} = \text{kg} \cdot \text{m/s}^2 = \text{kg} \cdot \text{m} \cdot \text{s}^{-2}\)
\(v\):車速 \(\text{m/s} = \text{m} \cdot \text{s}^{-1}\)(km/h表示の場合は、\(\frac{1}{3.6} \cdot v\) [\(\text{m} \cdot \text{s}^{-1}\)]を用いる)
駆動力曲線は、図13のA(1速)のように、1速の駆動力は大きいが、速度の範囲が狭く、左に片寄っている。
また、駆動力曲線はAからEになるにつれて次第に低く広くなってゆく。
なお、CVTなどの無段変速式トランスミッションの場合は、図のX曲線のようになる。
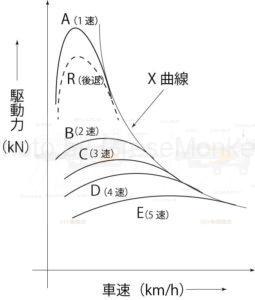
図13:前進5段変速式と無段変速式の場合の駆動力の関連
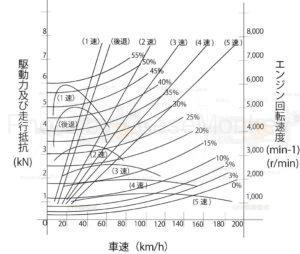
図11:走行性能曲線図
図11の走行性能曲線図において、0~55%の各線は上り坂の走行性能を示す曲線で、%は勾配の大きさを表している。
例えば、20%は\(tan\)\(\theta\)=0.2(\(\theta\)は勾配角)の勾配を示しており、0%の線は平坦な路面の走行抵抗を示す曲線で、転がり抵抗と空気抵抗の和である。
最高速度

図11:走行性能曲線図
自動車の最高速度は、一般に変速比の最も小さいギヤで平坦な路面を走行するときの駆動力曲線と走行抵抗曲線の交点をいう。
したがって、図11の走行性能曲線図に示す性能の自動車では、5速の駆動力曲線と0%の走行抵抗曲線の交点から、最高速度は約165km/hであることがわかる。
加速性能

図11:走行性能曲線図
図11において、平坦な路面走行の場合を考えると、最高速度以下では駆動力は走行抵抗より大きいので、その差が余裕駆動力として加速に費やされることになる。
余裕駆動力は、1速が最も大きく、2、3、4、5速の順に小さくなるため、1速から5速にまで、適宜にシフトしていけば大きな加速度が得られる。
任意の速度で走行しているときの加速度は、走行性能曲線図から算出することができる。
加速度(\(\alpha\))と加速力(\(F\))との関係は
\(F = (M + M’)\alpha \, [\text{N}]\) または \(\alpha = \frac{F}{M + M’} \, [\text{m/s}^2]\) である。
例えば、図11において、3速で平坦な路面を70km/hで走行しているときの余裕駆動力は約1.7kNで。表4より自動車総質量は1225kgであるから、加速度は次のように計算することが出来る。
自動車質量 = \(1225 \, [\text{kg}] – 55 \, [\text{kg/人}] \times 5 \, [\text{人}] = 950 \, [\text{kg}]\) (自動車総質量 – 乗車質量)
\(M’\) を自動車質量の5%とすれば、
\(M’ = 950 \, [\text{kg}] \times 0.05 = 47.5 \, [\text{kg}]\)
よって \( \alpha = \frac{F}{M + M’} \, [\text{m/s}^2] \) より
加速度 \( \alpha = \frac{1.7 \times 10^3 \, [\text{kg} \cdot \text{m} \cdot \text{s}^{-2}]}{1225 \, [\text{kg}] + 47.5 \, [\text{kg}]} = \frac{1700 \, [\text{kg} \cdot \text{m} \cdot \text{s}^{-2}]}{1272.5 \, [\text{kg}]} \approx 1.34 \, [\text{m/s}^2]\)
\( \alpha = 1.34 \, [\text{m/s}^2] \)
したがって、加速性能を高めるためには、余裕駆動力を大きくすること(加速度が上がる)と自動車総質量を小さくすること(軽量化)が必要となってくることがわかる。
登坂能力
坂路を一定の速度で上っている場合
駆動力 – (転がり抵抗 + 空気抵抗) = \(F\) とすると
この力(\(F\))は、全てが勾配抵抗に費やされるので、
\(F = Mg\sin\theta\)
この式から、登坂可能な坂の勾配角度\(\theta\)を求めることが出来る。
また、走行性能曲線図において、各種勾配の走行抵抗の曲線と各変速段階の駆動力曲線との交点から、各変速段階において、その勾配を登りえる速度を求めることが出来る。

















