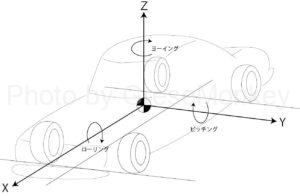
サスペンションと車体にかかる力 その2
慣性主軸
前回の記事「サスペンションと車体にかかる力」の要点
クルマが加速した場合にサスペンションアームに働く力の中で、加速によって発生する車体後部を下げようとする力であるスクワット力は、サスペンションアームの取り付け位置（セミトレーリングアーム式の場合は仮想の回転中心）を、適切な位置に設定することにより、ゼロにすることが可能であった。
その位置は、前輪中心にタイヤ半径と重心高さを加えた点と、後輪中心点を結んだ直線上にあった。
ただし、セミトレーリングアーム式の場合には、サスペンションの作動上の要求（タイヤのアライメント）やパッケージング上の制約（リヤシートやフロアなどの位置）から、アンチスクワットどころかむしろスクワット力を助長させるような位置に設定せざるを得なかった。
そこで今回は、この問題を解決できる可能性があるダブルウイッシュボーン式サスペンションについて最初に考えてみることから始めてみる。
目次
ダブルウイッシュボーン式サスペンションの場合
図1-1：ダブルウイッシュボーン式の回転中心
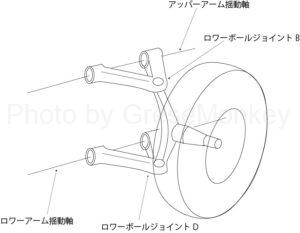
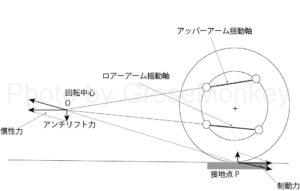
ダブルウイッシュボーン式の場合は、アッパーボールジョイントBはアッパーアームの揺動軸を中心に回転運動をおこない、ロワーボールジョイントDはロワーアームの揺動軸を中心に回転運動を行う。
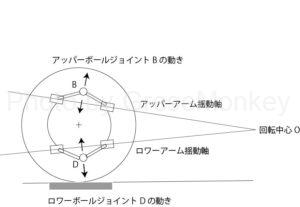
これを側面図（図1-2）でみた場合、アッパーボールジョイントBはアッパーアームの揺動軸に対して直角に上下運動し、ロワーボールジョイントDはロワーアームの揺動軸に対して直角な上下運動を行う事になる。
したがって、バブキャリア全体としては、アッパーアームとロワーアームの揺動軸をそれぞれ延長し、その延長線が交差する点を中心に回転運動をすることになる。（図1-2参照）
これはロールセンターを求めるときに求めた瞬間中心と同じ考え方である。
図1-1：ダブルウイッシュボーン式の回転中心
もしも、それぞれの揺動軸が路面と平行で交差しない場合には、回転中心Oの位置は無限の彼方になってしまうので、アンチダイブやアンチスクワットの特性は発生しないことになる。
厳密にはアッパーボールジョイントとロワーボールジョイントを通ってそれぞれの揺動軸に対して平行に直線を引き、この2本の直線が交差する点を回転中心Oとするべきである。
しかし、ボールジョイントの位置はホイールストロークによってその都度変化するので、回転中心Oをそれぞれの揺動軸の延長線が交差する点であるとしてもあまり変化はない。
他の方式のサスペンションでは、フロアやリヤシートなどに邪魔されて理想的な位置に回転中心を持ってくることが難しいのだが、ダブルウイッシュボーンの場合は、アッパーアームとロワーアームの揺動軸の位置や傾きを選択することによって、かなり自由に下層の回転中心を設定することが可能となる。これはサスペンションの形式がダブルウイッシュボーン式やマルチリンク式が多く採用されて主流になった理由のひとつである。
図2：ダブルウイッシュボーン式のアンチダイブ・ジオメトリー（前輪駆動時）
図3：ダブルウイッシュボーン式のアンチリフト・ジオメトリー（後輪駆動時）
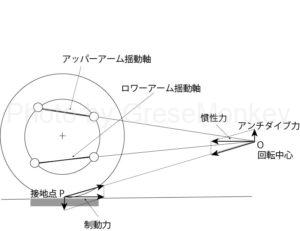
回転中心Oを求めた後の考え方は、トレーリングアーム式の場合と全く同じである。図2は制動時に発生する前輪側のアンチダイブ特性であり、図3は後輪側のアンチダイブ特性である。
ストラット式の場合
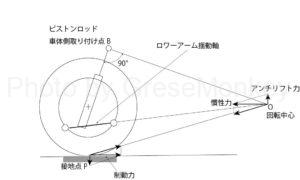
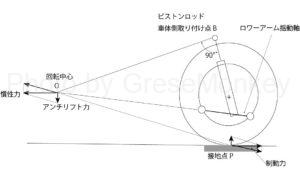
ストラット式の場合は、ストラットの車体側の取り付け点Bからピストンロッドと直角に直線を延ばし、ロアアームのよう同軸を延長した直線と交差した点が求める回転中心がOとなる。
回転中心Oを求めた後の考え方は、ダブルウイッシュボーン式やトレーディングアーム式の場合と全く同じになる。
図4：ストラット式アンチダイブ・ジオメトリー（前輪駆動時）
図5：ストラット式アンチダイブ・ジオメトリー（後輪駆動時）
図4は制動時に発生する前輪側のアンチダイブ特性で、図5は後輪側のアンチリフト特性である。
ただしストラット式の場合は、ロワーアームの揺動軸の位置や傾きはダブルウイッシュボーン式と同程度に選択することが可能であるが、ストラットの車体側の取り付け点の位置は、車体のレイアウト上の制限を受けてしまう。
例えば、リヤのストラットはリヤシートのシートバックを避けるために後傾させられるし。フロントのストラットは適正なキャスターとするために取り付け位置にはおのずと制約がかかってくる。
図6：回転中心が無限大の距離にある場合
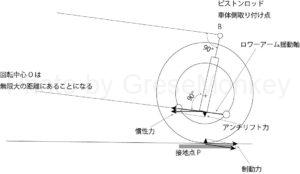
図6はストラットが後傾していて、ピストンロッドがロワーアームの揺動軸と直角な場合を表している。つまり、ピストンロッドと直角な直線がロワーアームのよう同軸と平行になり、回転中心Oの位置が無限の遠方になる場合である。
この場合は、回転中心Oがそばにある場合にに比べると多少効き目は劣るのだが、アンチリフトやアンチスクワットの特性を与えることができる。
すなわち、制動時には車輪が後方に引っ張られるので、車体側は前下方に動こうとしてアンチリフト特性が発生し、加速時には車輪が前進しようとするので、車体側は後上方に動こうとしてアンチスクワット特性が発生する。
これらは後輪側についての例であるが、同じように前輪側の場合は揺動軸が前下がりの前傾姿勢にすることによって、アンチダイブ特性を与えることができる。
制動時に働く力
図7：慣性力によるダイブとリフト
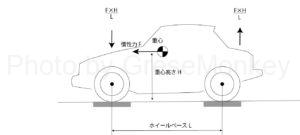
制動時に前が下がり、お尻を上げようとする力は車体の重心に走行時に発生した慣性力Fがかかることで発生する。（図7参照）
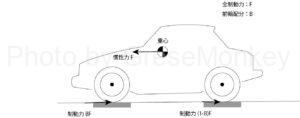
慣性力Fは制動力Fと同じ大きさであるが、この制動力は前輪と後輪で発生する制動力を足し算したものである。
しかしながら、前輪と後輪の制動力は同じではなく、制動時の荷重移動を考慮して、通常は前輪側が大きくなるように設定されている。
図8：前輪と後輪の制動力
この制動力の前輪側への配分は、一般に全制動力の60％〜70％程度であるが、仮にこの制動力をBとおくと、前輪側の制動力はB・Fとなり、後輪側の制動力は(1-B)・Fということになる。（図8参照）
ノーズダイブをゼロにする
図9：ダイブとリフトをゼロにする回転中心
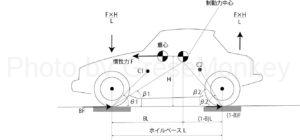
図9において、ホイールベースをL、重心の高さをHとすると、F×H/Lの力で前輪側を押し下げて、同時に同じ力で後輪側を持ち上げようとする。
ここで前輪側の回転中心をC1,路面とのなす角度をθ1とし、後輪側をそれぞれC2,θ2とすると、前輪側の制動力で発生する前輪側を持ち上げようとする力は、B・Ftanθ1になるので、前下がりの力（ノーズダイブ）をゼロにするには
$$
\frac{F×H}{L} = BF\tan\theta1
$$
$$
\frac{H}{B×L} = \tan\theta1
$$
ここで、図9より制動力中心と路面となす角度をβ1とすると、
$$
\frac{H}{B×L} = \tan\beta1 より
$$
$$
∴\tan\beta2 = \tan\theta2
$$
つまり、回転中心C1を制動力中心と前輪の接地点とを結んだ直線上に設定すれば、前下がりゼロ（ノーズダイブゼロ）のアンチダイブジオメトリーとなる。
θ1<β1ならばノーズダイブが生じることになる。
テールリフトをゼロにする
図9：ダイブとリフトをゼロにする回転中心
尻下がり（テールリフト）をゼロにするには、
$$
\frac{F×H}{L} = (1-B)F\tan\theta2
$$
$$
∴\frac{H}{(1-B)L} = \tan\theta2
$$
すなわち、回転中心C2を制動力中心と後輪の接地点とを結んだ直線上に設定すれば、テールリフトゼロのアンチリフトジオメトリーとなる。
ノーズダイブ時と同様に、θ2<β2ならばテールリフトが生じることになる。
引用元・参考文献・Webサイト